Cuádrica

Una superficie cuádrica es una superficie determinada por una ecuación de la forma: ${\displaystyle P(x_{1},x_{2}...x_{n})=0\ }$

donde P es un polinomio de segundo grado en las coordenadas ${\displaystyle x_{1},x_{2}...x_{n}\ }$.

Cuando no se precisa, es una superficie del espacio tridimensional real usual, en un sistema de coordenadas ortogonal y unitario, y las coordenadas se llaman x, y, z.

Historia

Fueron los matemáticos griegos de la antigüedad quienes iniciaron el estudio de las cuádricas, con el cono (una cuádrica) y sus secciones, que son las cónicas, curvas en un plano bidimensional, aunque no emplearon ecuaciones.

Definición algebraica

Una cuádrica o superficie cuádrica, es una hipersuperficie D-dimensional representada por una ecuación de segundo grado con variables (coordenadas) espaciales. Si estas coordenadas son ${\displaystyle \{x_{1},x_{2},...x_{D}\}\,}$, entonces la cuádrica típica en ese espacio se define mediante la ecuación algebraica:

${\displaystyle \sum _{i,j=1}^{D}Q_{i,j}x_{i}x_{j}+\sum _{i=1}^{D}P_{i}x_{i}+R=0}$

donde Q es una matriz cuadrada de dimensión (D), P es un vector de dimensión (D) y R es una constante. Si bien Q, P y R son por lo general reales o complejos, una cuádrica puede definirse en general sobre cualquier anillo.

Ecuación cartesiana

La ecuación cartesiana de una superficie cuádrica es de la forma:

${\displaystyle Ax^{2}+By^{2}+Cz^{2}+Dxy+Eyz+Fxz+Gx+Hy+Iz+J=0\,}$

• La definición algebraica de las cuádricas tiene el defecto de incluir casos sin interés geométrico y sin vínculo con el tema.

Por ejemplo, la ecuación:

${\displaystyle x^{2}+y^{2}+z^{2}+2xy+2yz+2xz=0\ }$

es de segundo grado pero, también se puede escribir como:

${\displaystyle (x+y+z)^{2}=0\ }$

que equivale a:

${\displaystyle x+y+z=0\ }$,

una ecuación de primer grado que corresponde a un plano, superficie que no tiene las propiedades relacionadas con el segundo grado. Generalmente, se descartan todos los polinomios de segundo grado que son cuadrados.

• A menudo, es útil recordar que si la ecuación en su forma cartesiana carece de términos cruzados, i.e., los coeficientes D, E y F son iguales a cero:

${\displaystyle D=0,E=0,F=0}$

entonces los términos lineales para cada variable:

${\displaystyle Gx,Hy,Iz}$

pueden asimilarse a los cuadráticos:

${\displaystyle Ax^{2},By^{2},Cz^{2}}$

mediante el método de completar cuadrados, de modo que sea fácil interpretar la ecuación como una de las formas "normalizadas" que se presentan a continuación, pero "descentrada" o "trasladada" (no centrada en el origen, ${\displaystyle (0,0,0)}$, sino en un punto de coordenadas implícitas en la nueva forma).

Ecuación normalizada

La ecuación normalizada de una cuádrica tridimensional (D = 3), centrada en el origen (0, 0, 0) de un espacio tridimensional, es:

${\displaystyle \pm {x^{2} \over a^{2}}\pm {y^{2} \over b^{2}}\pm {z^{2} \over c^{2}}\pm 1=0}$

Tipos de cuádricas

Por medio de traslaciones y rotaciones cualquier cuádrica se puede transformar en una de las formas "normalizadas". En el espacio tridimensional euclídeo, existen 16 formas normalizadas; las más interesantes son las siguientes:

a≠b≠c → elipsoide	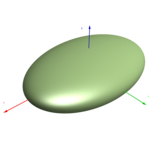${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}-1=0\,}$
a≠b → esferoide (caso particular de elipsoide)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over b^{2}}-1=0\,}$
esfera (caso particular de esferoide)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over a^{2}}-1=0\,}$
paraboloide
→ paraboloide hiperbólico (caso particular de paraboloide)	${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0\,}$
→ paraboloide elíptico (caso particular de paraboloide)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0\,}$
→ paraboloide circular (caso particular de paraboloide elíptico)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-z=0\,}$
hiperboloide
→ hiperboloide elíptico de una hoja (caso particular de hiperboloide)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}-1=0\,}$
→ hiperboloide circular de una hoja (caso particular de hiperboloide)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over c^{2}}-1=0\,}$
→ hiperboloide elíptico de dos hojas (caso particular de hiperboloide)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}+1=0\,}$
→ hiperboloide circular de dos hojas (caso particular de hiperboloide)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over c^{2}}+1=0\,}$
cilindro
→ cilindro elíptico (caso particular de cilindro)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-1=0\,}$
→ cilindro circular (caso particular de cilindro elíptico)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-1=0\,}$
→ cilindro hiperbólico (caso particular de cilindro)	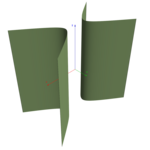${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-1=0\,}$
→ cilindro parabólico (caso particular de cilindro)	${\displaystyle x^{2}+2ay=0\,}$
cono elíptico	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,}$
→ cono circular (caso particular de cono elíptico)	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over c^{2}}=0\,}$

En el espacio proyectivo real, el elipsoide, el hiperboloide elíptico y el paraboloide elíptico son similares; los dos paraboloides hiperbólicos tampoco se diferencian entre ellos (por ser superficies regladas; el cono y el cilindro tampoco son distintos entre sí (por ser cuádricas "degeneradas"). En el espacio proyectivo complejo todas las cuádricas no degeneradas resultan indistinguibles entre ellas.

Véase también

• Cónica

Enlaces externos

• Cuádricas, en wmatem.eis.uva.es
• El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.