Flux

În matematică și fizică fluxul descrie cantitativ orice efect care pare să treacă sau să traverseze (fie că se mișcă sau nu) printr-o suprafață sau o substanță. Fluxul este un concept din matematica aplicată și calculul vectorial care are multe aplicații în fizică. Pentru fenomenele de transport, fluxul este o mărime vectorială, care descrie mărimea și direcția curgerii unei substanțe sau proprietăți. În calculul vectorial fluxul este o mărime scalară^⁠(d), definită ca integrala de suprafață a componentei perpendiculare a unui câmp vectorial de-a lungul suprafeței.

Terminologie

Termenul flux provine din latină fluxus, care înseamnă scurgere

Conceptul de flux termic a fost o contribuție cheie a lui Joseph Fourier, în analiza fenomenelor privind transmiterea căldurii. Tratatul său fundamental Théorie analytique de la chaleur (în română Teoria analitică a căldurii), definește „fluxul” ca o mărime centrală și continuă să obțină expresiile acum binecunoscute ale fluxului în termeni de diferențe de temperatură pe o placă și apoi, mai general, în termeni de gradienți de temperatură sau diferențe de temperatură, în alte geometrii. S-ar putea argumenta, pe baza lucrării lui James Clerk Maxwell, că definiția fluxului de transport precede definiția fluxului folosită în electromagnetism. Citatul specific din Maxwell este:

„În cazul fluxurilor, trebuie luată în considerare integrala, pe suprafață, a fluxului prin fiecare element al suprafeței. Rezultatul acestei operații se numește integrala de suprafață a fluxului. Reprezintă cantitatea care trece prin suprafață. ”

—James Clerk Maxwell

Conform definiției fluxului de transport, fluxul poate fi un singur vector sau poate fi un câmp vectorial / funcție de poziție. În acest din urmă caz, fluxul poate fi de-a lungul unei suprafețe. Prin contrast, conform definiției fluxului electromagnetic, fluxul este integrala de suprafață; nu are sens integrarea unui flux din a doua definiție pentru că ar fi integrarea de două ori de-a lungul suprafeței. Astfel, citatul lui Maxwell are sens doar dacă „fluxul” este utilizat conform definiției pentru transport (și, în plus, este mai degrabă un câmp vectorial decât un singur vector). Acest lucru este ironic pentru că Maxwell a fost unul dintre cei mai mari dezvoltatori ai ceea ce numim acum „flux electric” și „flux magnetic”, conform definiției fluxului electromagnetic. Numele lor în conformitate cu citatul (și definiția transportului) ar fi „la de suprafață a fluxului electric” și „integrala de suprafață a fluxului magnetic”, caz în care „fluxul electric” ar fi definit de fapt drept „câmp electric”, iar „fluxul magnetic” ar fi definit drept „câmp magnetic”. Acest lucru implică faptul că Maxwell a conceput aceste câmpuri ca un fel de fluxuri.

Având în vedere un flux conform definiției din electromagnetism, densitatea fluxului corespunzătoare, dacă se folosește acest termen, se referă la derivata sa pe suprafața de-a lungul căreia a fost integrat. După teorema fundamentală a calculului integral, densitatea fluxului corespunzătoare este, conform definiției pentru transport, un flux. Având în vedere un „curent” cum ar fi curentul electric — sarcină supra timp, „densitatea curentului” ar fi, de asemenea, un flux conform definiției pentru transport — sarcină supra timp și suprafață. Datorită definițiilor contradictorii ale „fluxului” și interschimbabilitatea lui „flux” și „curent” în exprimări netehnice, toți termenii folosiți în acest paragraf sunt uneori folosiți unii în locul altora și ambiguu. Fluxurile concrete din restul acestui articol vor fi utilizate în conformitate cu acceptarea lor largă în literatură, indiferent de definiția fluxului căreia îi corespunde termenul.

Fluxul drept curgere printr-o suprafață de o unitate

În fenomenele de transport^⁠(d) (transmiterea căldurii, transferul de masă și mecanica fluidelor), fluxul este definit drept „cantitatea de proprietate care curge în unitatea de timp prin unitatea de suprafață”și are dimensiunea ·⁻¹·⁻¹. „Suprafața” este cea „prin” care curge proprietatea. De exemplu, cantitatea de apă care curge printr-o secțiune transversală a unui râu în fiecare secundă împărțită la aria acelei secțiuni transversale, sau cantitatea de energie a luminii solare care cade într-o zonă de pe pământ în fiecare secundă împărțită la aria zonei, sunt tipuri de fluxuri.

Definiția matematică generală (pentru fluxul de transport)

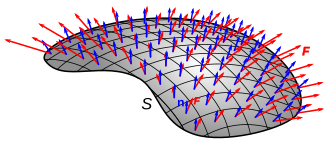
Iată 3 definiții în ordine crescătoare a complexității. Fiecare este un caz particular al versiunilor următoare. În toate cazurile sunt folosite simbolurile uzuale: j, (sau J) pentru flux, q pentru mărimea fizică care curge, t pentru timp și „A” pentru aria suprafeței. Acești identificatori se vor scrie cu caractere aldine atunci când și numai atunci când sunt vectori.

Prima, fluxul drept un (singur) scalar:

${\displaystyle j={\frac {I}{A}},}$

unde

${\displaystyle I=\lim _{\Delta t\to 0}{\frac {\Delta q}{\Delta t}}={\frac {\mathrm {d} q}{\mathrm {d} t}}.}$

În acest caz, suprafața prin care se măsoară fluxul este fixă și are aria A. Se presupune că suprafața este plană, iar debitul este pretutindeni constant în raport cu poziția și perpendicular pe suprafață.

A doua, fluxul drept un câmp scalar definit pe o suprafață, adică în funcție de punctele de pe suprafață:

${\displaystyle j(\mathbf {p} )={\frac {\partial I}{\partial A}}(\mathbf {p} ),}$

${\displaystyle I(A,\mathbf {p} )={\frac {\mathrm {d} q}{\mathrm {d} t}}(A,\mathbf {p} ).}$

Ca și înainte, se presupune că suprafața este plană și se presupune că fluxul este peste tot perpendicular pe ea. Însă valorile fluxului nu trebuie să fie aceleași. q este acum în funcție de p, un punct de pe suprafață și A, o zonă de pe suprafață. În loc să măsoare fluxul total prin suprafață, q măsoară fluxul printr-un disc cu aria A centrat pe p din suprafață.

A treia, fluxul drept un câmp vectorial:

${\displaystyle \mathbf {j} (\mathbf {p} )={\frac {\partial \mathbf {I} }{\partial A}}(\mathbf {p} ),}$

${\displaystyle \mathbf {I} (A,\mathbf {p} )={\underset {\mathbf {\hat {n}} }{\operatorname {arg\,max} }}\mathbf {\hat {n}} _{\mathbf {p} }{\frac {\mathrm {d} q}{\mathrm {d} t}}(A,\mathbf {p} ,\mathbf {\hat {n}} ).}$

În acest caz nu există nicio suprafață fixă prin care se măsoară. q este în funcție de punctele de pe suprfață, a ariei unei zone și a unei direcții (date de un versor ${\displaystyle \mathbf {\hat {n}} }$) și măsoară fluxul prin discul de aria A perpendiculară pe acel versor. I este definit prin alegerea versorului care maximizează fluxul în jurul punctului, deoarece fluxul adevărat este maximizat pe discul care este perpendicular pe acesta. Versorul maximizează astfel funcția în mod unic atunci când indică în „direcția adevărată” a fluxului. (Strict vorbind, acesta este un abuz de notație deoarece „arg max” nu poate compara direct vectori; se ia în loc vectorul cu cea mai mare normă.)

Proprietăți

Aceste definiții directe, în special ultima, sunt destul de greoaie. De exemplu, construcția arg max este artificială din perspectiva măsurătorilor empirice, când cu o giruetă sau altceva similar se poate deduce cu ușurință direcția fluxului într-un punct. În loc de definirea directă a fluxului vectorial, adesea este mai intuitiv să se precizeze unele proprietăți despre acesta. În plus, din aceste proprietăți, oricum fluxul poate fi determinat în mod unic.

Dacă fluxul j traversează zona la un unghi θ față de zona normală ${\displaystyle \mathbf {\hat {n}} }$, atunci produsul scalar este

${\displaystyle \mathbf {j} \cdot \mathbf {\hat {n}} =j\cos \theta .}$

Adică componenta fluxului care trece prin suprafață (adică normală acesteia) este j cos θ, în timp ce componenta fluxului care trece tangențial prin zonă este j sin θ, dar de fapt componenta tangențială a fluxului nu trece prin aria zonei. Singura componentă a fluxului care trece este componenta normală la zonă, adică componenta cosinus.

Pentru fluxul vectorial, integrala de suprafață a lui j de-a lungul suprafeței S dă curgerea adecvată în unitatea de timp prin suprafață:

${\displaystyle {\frac {\mathrm {d} q}{\mathrm {d} t}}=\iint _{S}\mathbf {j} \cdot \mathbf {\hat {n}} \,dA=\iint _{S}\mathbf {j} \cdot d\mathbf {A} ,}$

unde A (și infinitezimala sa) este aria orientată — combinația ${\displaystyle \mathbf {A} =A\mathbf {\hat {n}} }$ a ariei lui A prin care „trece” proprietatea și versorul ${\displaystyle \mathbf {\hat {n}} }$ normal la această zonă. Spre deosebire de al doilea set de ecuații, suprafața de aici nu trebuie să fie plană.

În final, se poate integra din nou pe durata de timp de la t₁ la t₂, obținând cantitatea totală a proprietății care a curs prin suprafață în acel timp (t₂ − t₁):

${\displaystyle q=\int _{t_{1}}^{t_{2}}\iint _{S}\mathbf {j} \cdot d\mathbf {A} \,dt.}$

Fluxuri de transport

Opt dintre cele mai comune forme de flux din literatura despre fenomenele de transport sunt definite după cum urmează:

1. Flux de impuls, rata de transfer a impulsului printr-o arie de o unitate (N·s·m⁻²·s⁻¹). (Legea lui Newton pentru viscozitate)
2. Flux termic , rata de căldură care trece printr-o arie de o unitate (J·m⁻²·s⁻¹). (Legea lui Fourier pentru conducția termică) (Definiția fluxului termic corespunde cu definiția originală a lui Maxwell.)
3. Flux difuziv, rata trecerii moleculelor printr-o arie de o unitate (mol·m⁻²·s⁻¹). (Legea lui Fick's privind difuzia)
4. Flux volumic, rata volumului care trece printr-o arie de o unitate (m³·m⁻²·s⁻¹). (Legea lui Darcy pentru curgerea apei în râuri^⁠(d))
5. Flux masic, rata masei care trece printr-o arie de o unitate (kg·m⁻²·s⁻¹). (O formă alternativă a legii lui Fick care include masa moleculară sau o formă alternativă a legii lui Darcy care include densitatea.)
6. Flux radiant, cantitatea de energie transferată de fotoni la o oarecare distanță de sursă printr-o arie de o unitate pe secundă (J·m⁻²·s⁻¹). Folosit în astronomie pentru a determina magnitudinea și clasa spectrală a unei stele. De asemenea, acționează ca o generalizare a fluxului termic, care este egal cu fluxul radiant atunci când este limitat la spectrul electromagnetic.
7. Flux de energie, rata de transfer a energiei printr-o arie de o unitate (J·m⁻²·s⁻¹). Fluxul radiant și fluxul termic sunt cazuri particulare ale fluxului de energie.
8. Flux de particule, rata de trecere a particulelor printr-o arie de o unitate ( m⁻²·s⁻¹)

Aceste fluxuri sunt vectori în fiecare punct din spațiu și au o mărime și o direcție definite. De asemenea, se poate lua divergența oricăruia dintre aceste fluxuri pentru a determina rata de acumulare a cantității într-un volum de control în jurul unui punct dat din spațiu. Pentru curgerile incompresibile^⁠(d) divergența fluxului volumic este zero.

Fluxul ca integrală de suprafață

Definiția matematică generală (pentru fluxul ca integrală de suprafață)

În calitate de concept matematic, fluxul este reprezentat de integrala de suprafață a unui câmp vectorial,

${\displaystyle \Phi _{F}=\iint _{A}\mathbf {F} \cdot \mathrm {d} \mathbf {A} }$

${\displaystyle \Phi _{F}=\iint _{A}\mathbf {F} \cdot \mathbf {n} \,\mathrm {d} A}$

unde F este câmpul vectorial, iar dA este aria vectorială a suprafeței A, poziționată ca suprafață normală. Pentru a doua relație, n este versorul orientat spre exteriorul suprafeței.

Suprafața trebuie să fie orientabilă, adică se pot distinge două aspecte: suprafața nu se pliază înapoi pe ea însăși. De asemenea, suprafața trebuie să fie orientată efectiv, adică să se folosească o convenție privind în care direcție curgerea este considerată pozitivă; apoi curgerea în sens invers este considerată negativă.

Normala la suprafață este de obicei direcționată conform regulii mâinii drepte.

Invers, se poate considera fluxul mărimea mai fundamentală și se poate numi câmpul vectorial „densitatea fluxului”.

Adesea un câmp vectorial este trasat de curbe (linii de câmp) care urmăresc „curgerea”; mărimea câmpului vectorial este atunci densitatea liniilor, iar fluxul printr-o suprafață este numărul de linii. Liniile provin din zone de divergență pozitivă (surse) și se termină în zone de divergență negativă (puțuri).

A se vedea și imaginea din dreapta: numărul de săgeți roșii care trec printr-o unitate de suprafață este densitatea fluxului, curba neagră care înconjoară săgețile roșii este limita suprafeței, iar orientarea săgeților față de suprafață este semnul produsului scalar al câmpului vectorial cu normalele la suprafață.

Dacă suprafața înconjoară o regiune tridimensională, de obicei suprafața este orientată astfel încât fluxul care intră în regiune este considerat pozitiv, iar cel ce iese negativ.

Teorema divergenței^⁠(d) afirmă că fluxul net care iese printr-o suprafață închisă din jurul unei regiuni tridimensionale este suma fluxurilor locale nete din fiecare punct al suprafeței (exprimat prin divergență).

Dacă suprafața nu este închisă, are ca frontieră o curbă orientată. Teorema lui Stokes afirmă că fluxul rotorului unui câmp vectorial este integrala curbilinie a câmpului vectorial de-a lungul frontierei. Această integrală este numită și circulație^⁠(d), în special în dinamica fluidelor. Astfel rotorul este densitatea circulației.

Fluxul și aceste teoreme au aplicații în multe discipline în care apar curenți, forțe etc., aplicate pe zone.

Electromagnetism

Flux electric

O „sarcină” electrică, cum ar fi un singur proton în spațiu, are o mărime definită în coulombi. O astfel de sarcină are în jurul ei un câmp electric. Intuitiv, câmpul electric dintr-o sarcină punctiformă pozitivă poate fi imaginat ca un punct care radiază linii de câmp electric (uneori numite și „linii de forță”). Conceptual, fluxul electric poate fi gândit ca „numărul de linii de câmp” care trec printr-o zonă dată. Matematic, fluxul electric este integrala componentei normale a câmpului electric dintr-o zonă dată. Prin urmare, unitățile de flux electric sunt, în Sistemul MKfS, newtoni ori pe coulomb. N m²/C. (Densitatea fluxului electric este fluxul electric printr-o unitate de suprafață și este o măsură a puterii componentei normale a câmpului electric mediu pe zona de integrare. Unitățile sale sunt N/C, la fel ca și în MKfS.)

Sunt folosite două tipuri de flux electric, unul pentru câmpul electric E:

${\displaystyle \Phi _{E}=}$ ${\displaystyle {\scriptstyle A}}$ ${\displaystyle \mathbf {E} \cdot {\rm {d}}\mathbf {A} }$

și altul pentru câmpul D (inducția electrică):

${\displaystyle \Phi _{D}=}$ ${\displaystyle {\scriptstyle A}}$ ${\displaystyle \mathbf {D} \cdot {\rm {d}}\mathbf {A} }$

Aceaste mărimi apar în teorema lui Gauss^⁠(d) – care afirmă că fluxul câmpului electric E printr-o suprafață închisă este proporțional cu sarcina electrică Q_A închisă de suprafață (independent de modul în care este distribuită sarcina). Forma integrală este:

${\displaystyle {\scriptstyle A}}$ ${\displaystyle \mathbf {E} \cdot {\rm {d}}\mathbf {A} ={\frac {Q_{A}}{\varepsilon _{0}}}}$

unde ε₀ este permitivitatea electrică a vidului^⁠(d).

Dacă se consideră fluxul vectorului câmpului electric, E, pentru un tub în apropierea unei sarcini punctuale din câmpul de sarcini, dar care nu are frontierele formate din linii tangente la câmp, fluxul prin frontiere este zero și există un flux egal și opus la ambele capete ale tubului. Aceasta este o consecință a teoremei lui Gauss aplicată unui câmp pătrat invers. Fluxul din orice secțiune transversală a tubului va fi același. Fluxul total pentru orice suprafață care înconjoară o sarcină q este q/ε₀.

În vid inducția electrică este dată de relația D = ε₀ E, deci pentru orice suprafață de delimitare fluxul câmpului D este egal cu sarcina Q_A în interiorul acesteia. Aici expresia „fluxul lui” indică o operație matematică și, după cum se poate observa, rezultatul nu este neapărat un „flux”, deoarece nimic nu curge de fapt de-a lungul liniilor câmpului electric.

Flux magnetic

Densitatea fluxului magnetic (câmpul magnetic) având unitatea Wb/m² (Tesla) se notează cu B și fluxul magnetic sunt definite analog:

${\displaystyle \Phi _{B}=\iint _{A}\mathbf {B} \cdot \mathrm {d} \mathbf {A} }$

cu aceeași notație de mai sus. Mărimea apare în legea inducției electromagnetice, unde fluxul magnetic este dependent de timp, fie pentru că frontiera este dependentă de timp, fie pentru că câmpul magnetic este dependent de timp. În formă integrală:

${\displaystyle -{\frac {{\rm {d}}\Phi _{B}}{{\rm {d}}t}}=\oint _{\partial A}\mathbf {E} \cdot d{\boldsymbol {\ell }}}$

unde dℓ este un vector infinitezimal pe curba închisă ${\displaystyle \partial A}$, cu norma egală cu lungimea elementului infinitesimal al liniei și direcțiea dată de tangenta la curba ${\displaystyle \partial A}$, cu semnul determinat de direcția de integrare.

Rata temporală de schimbare a fluxului magnetic printr-o buclă de sârmă este minus forța electromotoare creată în acel fir. Direcția este de așa natură încât, dacă se permite curentului să treacă prin fir, forța electromotoare va provoca un curent care „se opune” modificării câmpului magnetic, producând un câmp magnetic opus schimbării. Aceasta este baza pentru inductoare și multe generatoare electrice.

Flux Poynting

Fluxul vectorului Poynting^⁠(d) S printr-o o suprafață dată este viteza cu care energia electromagnetică traversează acea suprafață, definită ca înainte:

${\displaystyle \Phi _{S}=}$ ${\displaystyle {\scriptstyle A}}$ ${\displaystyle \mathbf {S} \cdot {\rm {d}}\mathbf {A} }$

Fluxul vectorului Poynting printr-o suprafață este puterea electromagnetică, sau energia care trece prin acea suprafață în unitatea de timp. Acesta este folosit în mod obișnuit în analiza radiației electromagnetice, dar are aplicații și în alte sisteme electromagnetice.

În mod confuz, vectorul Poynting este uneori numit flux de putere, care este un exemplu de flux de transport (v. mai sus). Unitatea de măsură este wați pe metru pătrat (W/m²).

Note

Bibliografie

• en Browne, Michael, PhD (2010). Physics for Engineering and Science, 2nd Edition. Schaum Outlines. New York, Toronto: McGraw-Hill Publishing. ISBN 978-0-0716-1399-6. 
• en Purcell, Edward, PhD (2013). Electricity and Magnetism, 3rd Edition. Cambridge, UK: Cambridge University Press. ISBN 978110-7014022. 

Lectură suplimentară

	Portal Fizică
	Portal matematică

• en Stauffer, P.H. (2006). „Flux Flummoxed: A Proposal for Consistent Usage”. Ground Water. 44 (2): 125–128. doi:10.1111/j.1745-6584.2006.00197.x. PMID 16556188.